Proposición: Enunciado de un hecho , como ley o un principio que se puede desmostrar.
Axioma: Es una proposición en que su verdad no llega a ser axioma no necesita demostración.
Teorema: Es una proposición que necesita ser demostrada.
Problema: Es una cuestión que se propone a ser resuelta.
Corolario: Es una proposición que es consecuencia de otra.
Axiomas básicos
1- El espacio tiene infinitos puntos, rectas y planos.
2- El plano tiene infinitos puntos y rectas.
3- La recta tiene infinitos puntos.
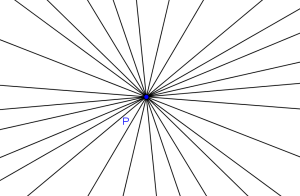
4- Por un punto pasan infinitas rectas.
5- Por una recta pasan infinitos planos.
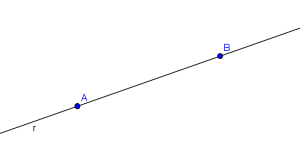
6- Por dos puntos pasa una única recta.
7- Por tres puntos no alineados pasa un único plano.
En este caso debemos aclarar que significa alineados. Tres puntos están alineados si pertenece a una misma recta.
8- Si dos puntos pertenecen a un plano, la recta que pasa por esos dos puntos también se encuentra en el mismo plano.
- Dados dos puntos se puede trazar una y solo una recta que los une.
- Cualquier segmento puede prolongarse de manera continua en cualquier sentido.
- Se puede trazar una circunferencia con centro en cualquier punto y de cualquier radio.
- Todos los ángulos rectos son congruentes.
- Si una recta, al cortar a otras dos, forma ángulos internos menores a dos ángulos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están los ángulos menores que dos rectos.
Este último postulado, que es conocido como el postulado de las paralelas, fue reformulado como:
- 5. Por un punto exterior a una recta, se puede trazar una única paralela a la recta dada.
Dos angulos opuestos por el vértice son iguales.
desmostrar que el ángulo alfa es igual al ángulo beta.
Por ángulos suplementarios
ángulo beta + ángulo alfa = 180°
ángulo gama + su opuesto = 180°
Por lo tanto el ángulo alfa = al ángulo beta.
l.q.q.d
Teorema 2.
Si dos lados de un triangulo y el ángulo comprendido son respectivamente iguales a dos lados y el angulo comprendido de otro triángulo , los dos triangulos son iguales .
Demostrar: El triángulo ABC = Triángulo XYZ
Sobreponemos el triángula ABC sobre el triángulo XYZ para qie A caiga sobre X y AB sobre XY.
Entonces B caera sobre Y
AC tomara la dirección de XZ
Suponemos que el ángulo A = ángulo X
C caerá en Z
suponemos que AC= XZ
Por lo tanto Cb coincidira con ZY "por dos puntos dados cualesquiera puede hacerse pasar un arecta y solo una"
Por lo tanto los dos triángulos son iguales.
Teorema 3
Dos triángulos son iguales si tienen iguales respectivamente un lado y los angulos adyacentes a ese lado.
Demostrar que : Triangulo ABC= Triángulo XYZ.
Colocamos en triángulo ABC sobre el triángulo XYZ para que AB coincida en XY. Por post 5
Los lados AC y BC tomarán respectivamente las direcciones de XZ y YZ .
Por lo tanto C caerá sobre Z por colorario 2
Por lo tanto los dos triángulos son iguales " Dos figuras son iguales cuando se pueden hacer coincider en todas sus partes".
Teorema 4:
En tos triangulo isoceles los ángulos opuestos a los lados iguales son iguales.
Demotrar que: angulo A = ángulo B
Trasamos la bisectriz CD del ángulo ACb en los triángulos ACD, BDC
POr hip:
AC=BC
CD=CD por lado común
ángulo ACD= ángulo DCB por construcción
Por lo tanto el triángulo ACD= triángulo BCD por colorario 67 " las partes homólogas de dos figuras congruentes son iguales"
Teorema 5.
Si dos ángulos de un triángilo son iguales, los lados opuestos son iguales, y el triángulo por lo tanto es isósceles.
demostrar que: AC = BC
Suponemos que el Triángulo A´B´C´C´ es el triangulo ABC en otra posición
Volteamo el triángulo A´B´C´ sobre el ABC para que B´Caiga en A y A´en B
El ángulo A´= ángulo B´
El ángulo A = ángulo A´
Por lo tanto el ángulo A = ángulo B´
por lo tanto B´C´tomará la dirección de AC.
Luego C´caerá a su vez en AC y BC y por tanto en C
Por lo tanto B´C´ = AC
Pero B´C´ caerá a la vaz en BC
por lo tanto BC = AC.
Todo triángulo equiángulo es equilatero.
Teorema 6.
Si los tres lados de un triángulo son respectivamente iguales a los trees lados de otro , los dos triángulos son iguales.
Demostrar que: el triángulo ABC = A´B´C´
Sean AB y A´B´ lados mayores de los dos triángulos .
Volteése en triángulo A´B´C´ y coloquese de modo que A´B ´ coincida con su igual AB .
El vertice caerá abajo del lado AB , como se ve , y por tanto el triábgulo A´B´C´quedará en la posición ABC´
Tracesé CC´
AC= AC´ , BC = BC´ por hipo.
El ángulo ACC´= CC´A , y el ángulo CC´B= BC´C por teorema 4
El ángulo ACC´+C´CB= CC´A+BC´C por axioma1
El ángulo ABC = BCÁ por axioma 8
El triángulo ABC = ABC´ por teorema 2
Por lo tanto El triángulo ABC = A´B´C´
Teorema 7:
Si de un punto situado en el interior de un triángulo se trazan dos rectas a los extremos de uno de los lados , la suma de estas rectas es menor qie la sima de los tros dos lados del triángulo.
Demostrar que : CA+CB mayor que PA+ PB
Prolongamos AP hasta su intersección Q con el lado CB
CA+CQ mayor que PA+PQ Por postulado3
BQ+PQ mayor que PB ´por post 3
Sumamos las desigualdades nos queda que: CA+CQ+BQ.+PQ mayor que PA+PQ+PB Por axioma 8
No queda que PQ de los dos miembros de la desigualdad es : CA+CB mayor que PA+PB
Teorema 8:
De un punto exterior a una recta no puede bajarse a esa recta mas de una perpendicular.
Demostrar que PZ no es la perpendicular a XY .
Prolongamos PO hasta P´, haciendo OP´ igual a la perpendicular OP. Por post 2
Trácese P´Z Por post 1
Por contrucción , POP´ es un a recta
Por lo tanto PZP´no es uuna recta. Por post 1
Por lo tanto el ángulo P´ZP no es de lados colineales.
El ángulo POZ y el POP´ son rectos "Una recta es perpendicular a otra si los ángulos una con la otra son rectos ."
PO=OP´ por contrucción
OZ = OZ por igualdad.
Por lo tanto el triángulo OPZ= OP´Z por teorema 2.
El ángulo OZP = OZP´ Las parte homólogas de figuras congruentes son iguales.
Por Lo tanto el ángulo OZP mitad del P´ZP no es recto "un ángul orecto es la mitad de un ángulo del lados colineales"
Por lo tanto PZ no es perpendicular a XY .
Teorema 9:
Si de un punto de una perpendicular a una recta se trazan a la recta dos oblicuas cuyos pies esten a igual distancia del pie de la perpendicular , esas dos oblicuas son iguales y forman ángulos iguales con la perpendicular.
Demostrar que: PA= PB , y el ángulo APO= BOP
En los triángulños AOP , BOP los ángulos POA y BOP son rectos.
Por lo tato el ángulo POA = POB por colorario 3.
OA=OB
PO=PO Por identidad
Por lo tanto el triángulo AOP = BOP Por teorema 2
Por lo tanto PA= PB
ángulo APO= BPO " las partes homologas de dos figuras congruentes son iguales"
Teorema 10:
Deun punto perpendicular a una recta se traza a esa recta dos oblicuas cuyos pies no equidisten de la perpendicular , la oblicua cuyo pie dista más es mayor que la otra.
Demostrar que: PA es mayor que PC.
OB= OC y trazamos PB..
PB= PC por teorema 9
En PO que prolongamos tomamos OP´=OP y trazamos P´A,P´B
PA=P´A y PB= P´B Por teorema 9.
PA+ P´A mayor que PB+ P´B Por teorema 7
Por lo tanto 2PA mayor que 2PB y PA ,mayor que PB por axima 8 y 4.
Por lo tanto PA mayor que PC por colorario 8.
Teorema 11:
La perpendicular es la mas corta de las rectas que puieden trazarse a una recta de un punto situado fuera de ella.
demostrar que PO mayor que PZ.
Prolongamos PO hasta P´ para que OP´ sea igual a PO , y trazamos P´Z .
PZ= P´Z por teorema 9
por lo tanto PZ+P´Z= 2PZ Por axioma 8.
PO+P´O= 2PO Por axioma 8.
PO +P´O menor que PZ+P´Z por postulado 4.
Por lo tanto 2PO menor que 2PZ Por axioma 8.
PO menor que PZ Por axioma 5
 .
.









No hay comentarios:
Publicar un comentario